枫落的Blog
0%

感知机 Perceptron

发表于 更新于 分类于

感知机是二类分类的线性分类模型，即输出为 和 二值，属于判别模型。感知机学习旨在将训练数据进行线性划分，有简单易实现的优点。感知机算法分为原始形式和对偶形式。

感知机模型的函数表示为

其中 为输入的实例的特征向量， 为输出的实例的类别。 和 为感知机模型参数， 叫做权值（weight）或权值向量， 叫做偏值（bias）， 表示 和 的内积。

sign 是符号函数，即

感知机模型的假设空间是定义在特征空间的所有线性分类模型，即函数集合 。

（假设空间是指所有可能的模型的集合）

感知机可以理解为：所有训练样本在一个特征空间中， 是特征空间中的一个超平面 ，它将特征空间划分为两个部分（正、负两类）。这个超平面 称为分离超平面（separating hyperplane）。

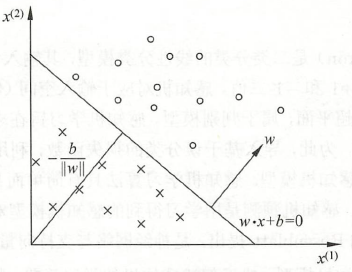
image-20201023030026330

假设训练数据集是线性可分的（即可以找到超平面 将正负实例点完全分开），为了找到超平面 ，我们可以定义一个（经验）损失函数并将损失函数极小化。（经验损失函数表示由所有训练样本的误差计算得到的损失函数）

感知机采用的损失函数是误分类点到超平面 的总距离。首先，特征空间中任意一点 到超平面 的距离为：

其中， 是 的 范式。

其次，对误分类的数据 ， 成立。

因此，误差分类点 到超平面 的距离是

于是，假设超平面 的误分类点集合为 ，那么所有误分类点到超平面 的总距离为

不考虑 ，就得到感知机学习的 损失函数。

所以，感知机学习的损失函数为

显然，损失函数 。如果没有误分类点，损失函数为 0。误分类点越少，损失函数越小。于是我们需要选取使损失函数最小的模型参数 和 。

接下来是之前提到的两种感知机学习的算法：原始形式和对偶形式。

原始形式

已知感知机学习是找到使损失函数极小化的模型参数，即

所以感知机学习算法是由误分类驱动的，具体采用 随机梯度下降法：首先，任意选取一个超平面（即任意选取参数 和 ），然后用梯度下降法不断地极小化目标函数（即损失函数）。在极小化过程中，每次随机选取一个误分类点使其梯度下降。

损失函数的梯度为

随机选取一个误分类点 ，对 和 进行更新：

其中 是步长，又称为 学习率（learning rate）。

于是，感知机学习算法的 原始形式 为：

  • Input：训练数据集 ，学习率 ；
  • Output：，，感知机模型 。

  1. 选取随机初始参数 和 ；

  2. 选取训练集中样本 ；

  3. 如果 ，

  4. 重复 2、3 步，直到训练集中没有误分类点。

选择不同的初始参数，或者以不同的顺序选取误分类点，会得到不同的解。

根据定理 Novikoff 可知，误分类的次数是有上限的，所以经过有限次搜索可以找到将训练集完全正确分开的超平面。但为了得到唯一的超平面，需要对超平面增加约束条件，这就是线性支持向量机的想法。

对偶形式

对偶形式的基本想法是，将 和 表示为实例 和标记 的线性组合的形式，通过求解其系数从而求得 和 。

还是取初始值 和 ，误分类点通过

修改 和 。

假设修改 次，则 和 关于 的增量分别是 和 ，这里 。于是，最后学习得到的模型参数可表示为

这里 。当 时，表示第 个实例由于误分而进行更新的次数。实例更新次数越多，意味着它离超平面越近，也就越难正确分类。这样的实例对学习结构影响最大。

感知机学习算法的 对偶形式 为：

  • Input：训练数据集 ，学习率 ；
  • Output：，，感知机模型 ，其中 。

  1. 令 ，；

  2. 选取训练集中样本 ；

  3. 如果 ，

    （** 注意！** 这里的判断公式可以进行变形：

    ​ 将上面的公式 带入 得到

    ​

    ​ 合并后变为

    ​

    ​ 在代码中我使用这个公式进行判断，因为如果直接用 会导致结果错误，这点我也不太清楚原因）

  4. 重复 2、3 步，直到训练集中没有误分类点。

对偶形式中训练实例只以内积的形式出现，可以先将所以训练数据的内积计算出来以矩阵形式储存，这就是 Gram 矩阵

（在对偶形式的应用中，，其中 ）

在选择误分类点顺序一致时，对偶形式的解与原始形式一样。并且，对偶形式也存在多个解。

代码实现

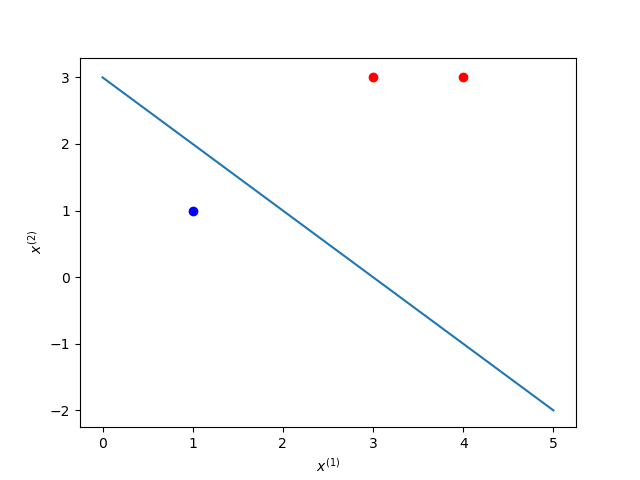
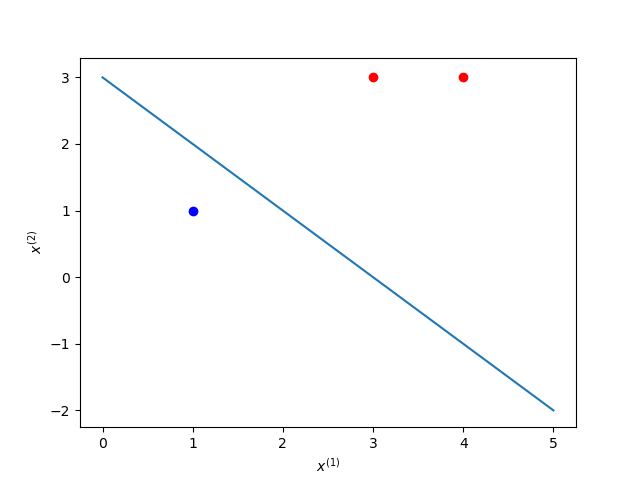
已知正样本点 ，，负样本点 ，求感知机模型。

原始形式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class PerceptronOrigin():
    '''
    感知机算法的原始形式
    '''
    def __init__(self, x, y, a=1):
        self.x=x
        self.y=y
        # 初始化模型参数 w 和 b （这里将它们都设为 0）
        self.w=np.zeros(x.shape[1])
        self.b=0
        # 学习率
        self.a=a

    def train(self):
        '''
        找出不会误分类任何训练样本的超平面
        :return: w, b
        '''
        error_exist=True
        current=0
        index_point=0
        while error_exist:
            # 如果存在误分类点，更新参数
            if (np.dot(self.x[current],self.w)+self.b)*self.y[current]<=0:
                index_point=current
                self.w=np.add(self.w,self.a*self.y[current]*self.x[current])
                self.b+=self.a*self.y[current]
            else:
                # 当前误分类点被正确分类后，从该点开始遍历所有点
                current=(current+1)%self.x.shape[0]
                # 直到索引再次回到该点，表示已无误分类点
                if current==index_point:
                    error_exist=False
        return self.w,self.b

    def predict(self, x):
        '''
        对测试样本进行预测
        :param x: input(feature) space
        :return: output label (+1 or -1)
        '''
        y=np.dot(self.w,x)+self.b
        return int(y)

Figure_1.png

对偶形式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class PerceptronDual():
    def __init__(self, x, y, a=1):
        self.x=x
        self.y=y
        self.w=np.zeros(x.shape[1])
        self.eta=np.zeros(x.shape[0])
        self.b=0
        self.a=a

    def get_Gram(self):
        '''
        计算 Gram 矩阵
        '''
        x=self.x.copy()
        G=x.dot(x.T)
        return G

    def train(self):
        G=self.get_Gram()
        error_exist = True
        current = 0
        index_point = 0
        while error_exist:
            if self.y[current]*(sum((self.eta[i]*self.y[i]*(G[current][i]+1)) for i in range(self.y.shape[0]))) <=0:
                ''' 注意这个判断公式 '''
                index_point = current
                self.eta[current]+=self.a
                self.b+=self.a*self.y[current]
            else:
                current=(current+1)%self.x.shape[0]
                if current==index_point:
                    error_exist=False
        
        for i in range(self.y.shape[0]):
            ''' 用公式计算出参数 w '''
            self.w=np.add(self.w,(self.eta[i]*self.x[i]*self.y[i]))
        return self.w,self.b

    def predict(self, x):
        y=np.dot(self.w,x)+self.b
        return int(y)

Figure_2.png

完整代码

参考文献

[1] 《统计学习方法（第二版）》李航

[2] 【机器学习笔记】——感知机（Perceptron）